Fonctions et Limites
Limite d'une fonction Soit f une fonction
f est continue en 0 alors f est forcément derivable est 0
Vrai Faux
Pour que f ait une limite en 0 il faut que f soit definie en 0
Vrai Faux
, mais d'après le cours elle admet une limite en 0.
Limites infinies et limites infinies
Remplir les blancs par les reponses adéquates.
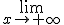(4x-8)/(3x+10) vaut
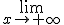(x+1)/x vaut
Fonction négligeables par rapport à une autreSoit deux fonctions F(x)=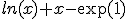
et G(x)=
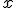et soit H(x)=-sin(x) et I(x)=cos(x)
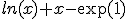et G(x)= 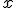et soit H(x)=-sin(x) et I(x)=cos(x)
Au voisinage de exp(1), G(x)=o(F(x))
Vrai Faux
G(x)/F(x), en la resolvant on s'apercoit que cette limite vaut e et non 0 donc F(x) non négligeable devant G(x).
Au voisinage de 3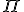
/4, H(x) est équivalente à I(x)
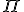/4, H(x) est équivalente à I(x)
Vrai Faux
et -sin(3
Asymptotes et branches infiniesOn dit qu'une fonction :
admet une asymptote horizontale si sa limite en un point est infinie
Vrai Faux
admet une asymptote verticale si sa limite en un point est infinie
Vrai Faux
est asymptote à une autre si et seulement si 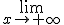(f(x)-g(x))=x
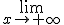(f(x)-g(x))=x
Vrai Faux
Paraboles Asymptotessoit F(x) = 4x²+8x+12 quelle est à sa parabole asymptote G(x) en +l'infini ?
|
G(x) = 2x+8
| |
|
G(x) = 
| |
|
G(x)=4x²+8x+k
|